Introduction to Derivatives

Summary:

Introduction to Derivatives introduces the concept of derivatives and their applications in calculus. The chapter begins by discussing the motivation behind studying derivatives, focusing on two classical problems: finding the tangent to a curve and determining the instantaneous velocity of a moving object.

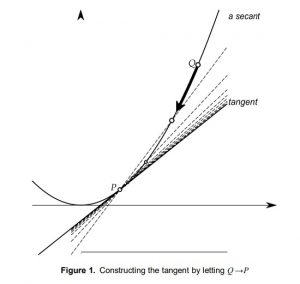
To find the tangent to a curve, the chapter explains constructing a secant line between two points on the graph and taking the limit as the points get closer together, resulting in the tangent line at a specific point. It uses the example of a parabola to illustrate this process.

Next, the concept of instantaneous velocity is explored. It highlights the challenge of defining velocity in an instant since it involves dividing zero by zero. The chapter explains how to calculate average velocity over a small interval and then take the limit as the interval approaches zero to find the instantaneous velocity.

The chapter also introduces the idea of rates of change and how they are related to derivatives. It demonstrates how the rate of change of a function can be computed by finding the difference quotient and taking the limit as the interval approaches zero. Examples of rates of change in different contexts, such as acceleration and chemical reactions, are provided.

Excerpt:

Introduction to Derivatives

Derivatives (1)
To work with derivatives, you have to know what a limit is, but to motivate why we are going to study limits, let’s first look at the two classical problems that gave rise to the notion of a derivative: the tangent to a curve, and the instantaneous velocity of a moving object.

1. The tangent to a curve
Suppose you have a function y = f (x), and you draw its graph. If you want to find the tangent to the graph of f at some given point on the graph of f, how would you do that?

Introduction to Derivatives