Functions Explained

Summary:

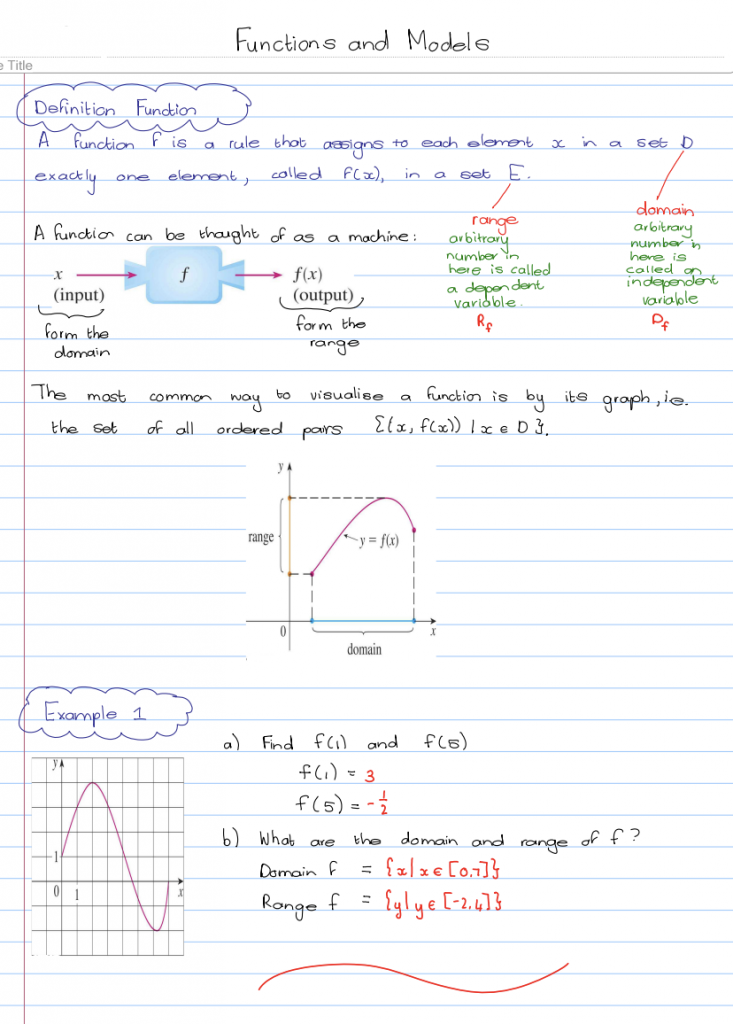
This comprehensive note provides a detailed explanation of various aspects of functions, covering topics such as increasing and decreasing functions, linear models, polynomials, power functions, rational functions, logarithmic functions, trigonometric functions, algebraic functions, function translation and reflection, and combinations of functions. The note includes examples to aid in understanding and application of these concepts.

Excerpt:

Functions Explained

Linear models are introduced as a special type of function that a straight line can represent. The note highlights their significance in modelling real-world phenomena with a constant rate of change.

Polynomials, including linear, quadratic, cubic, and higher-order polynomials, are examined regarding their degree and leading coefficients. The note explains the key properties of these functions and their graphical representations.

Power functions, which are functions of form f(x) = ax^n, where a is a constant and n is a real number, are discussed. The note explores the behaviour of power functions based on the value of the exponent, identifying whether they are increasing or decreasing and their concavity.

Rational functions, which are ratios of two polynomial functions, are explored in terms of their domains, asymptotes, and the behaviour of the numerator and denominator.

The note delves into logarithmic functions, emphasizing their inverse relationship with exponential functions. It explains the properties of logarithmic functions, including their domains, ranges, and asymptotic behaviour.

Trigonometric functions, such as sine, cosine, and tangent, are examined, focusing on their periodic nature and graphical representations. The note discusses their key properties and how they can be used to model various natural phenomena.

Algebraic functions, which are functions that can be constructed using algebraic operations like addition, subtraction, multiplication, division, and composition, are explored. The note provides examples of algebraic functions and demonstrates how they can be combined and manipulated.

Function translation and reflection are discussed, highlighting how shifts and reflections in the coordinate plane affect the graph of a function. The note explains how changes in the equation of a function can result in shifts along the x-axis, y-axis, or both.