Differential Equations (Grade A)
Summary:
The note summarises the first two lectures of the course Differential Equations (MTH401). In Lecture #1, the background of linear, quadratic, cubic and systems of linear equations is discussed along with algebra, trigonometry, calculus, differentiation, integration, inverse trigonometric functions, and their applications. Lecture #2 covers the fundamentals of differential equations, including their definition, classification, solution, initial value problems, and the existence and uniqueness of solutions. It is mentioned that the theory of differential equations is applicable to various fields such as physics, chemistry, engineering, medicine, and biology. The note also provides specific examples of ordinary differential equations (ODEs) and partial differential equations (PDEs).
Excerpt:
Differential Equations
Lecture#1
Background
Linear y=mx+c
Quadratic ax2+bx+c=0
Cubic ax3+bx2+cx+d=0
Systems of Linear equations
ax+by+c=0
lx+my+n=0
Solution?
Equation
Differential Operator
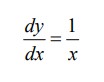
Differential Equations
Taking anti-derivative on both sides
y=ln x
From the past:
- Algebra
- Trigonometry
- Calculus
- Differentiation
- Integration
- Differentiation
- Algebraic Functions
- Trigonometric Functions
- Logarithmic Functions
- Exponential Functions
- Inverse Trigonometric Functions
- More Differentiation
- Successive Differentiation
- Higher Order
- Leibnitz Theorem
- Applications
- Maxima and Minima
- Tangent and Normal
- Partial Derivatives
- y=f(x)
f(x,y)=0
z=f(x,y)
- y=f(x)
- Integration
- Reverse of Differentiation
- By parts
- By substitution
- By Partial Fractions
- Reduction Formula
- Frequently required
- Standard Differentiation formulae
- Standard Integration Formulae
- Differential Equations
- Something New
- Mostly old stuff
- Presented differently
- Analyzed differently
- Applied Differently
…..
Lecture-2:
Fundamentals
- Definition of a differential equation.
- Classification of differential equations.
- Solution of a differential equation.
- Initial value problems associated with DE.
- Existence and uniqueness of solutions.
Elements of the Theory
- Applicable to:
• Chemistry
• Physics
• Engineering
• Medicine
• Biology
• Anthropology - Differential Equation – involves an unknown function with one or more of its derivatives
- Ordinary D.E. – a function where the unknown is dependent upon only one independent variable
…
Lecture-10
Applications of First-Order Differential Equations
In order to translate a physical phenomenon in terms of mathematics, we strive for a set
of equations that describe the system adequately. This set of equations is called a Model
for the phenomenon. The basic steps in building such a model consist of the following
steps:
Step 1: We clearly state the assumptions on which the model will be based. These assumptions should describe the relationships among the quantities to be studied.
Step 2: Completely describe the parameters and variables to be used in the model.
Step 3: Use the assumptions (from Step 1) to derive mathematical equations relating the parameters and variables (from Step 2).


Reviews