Derivatives Explained

Summary:

This comprehensive note provides a detailed explanation of derivatives, their definitions, and their various applications. Derivatives play a fundamental role in calculus, allowing us to analyze rates of change, velocities, and the behaviour of functions. The note covers topics such as the instantaneous rate of change, the derivative as a function, notations, higher derivatives, differentiation formulae, a derivative of trigonometric functions, the chain rule, and implicit differentiation, and includes relevant proofs and theoretical explanations.

The note begins by defining derivatives as the measure of the rate at which a function changes with respect to its independent variable. It explores the concept of velocities, explaining how derivatives can be used to determine instantaneous velocities at any given point. This fundamental understanding sets the stage for further exploration of derivatives in the context of rates of change.

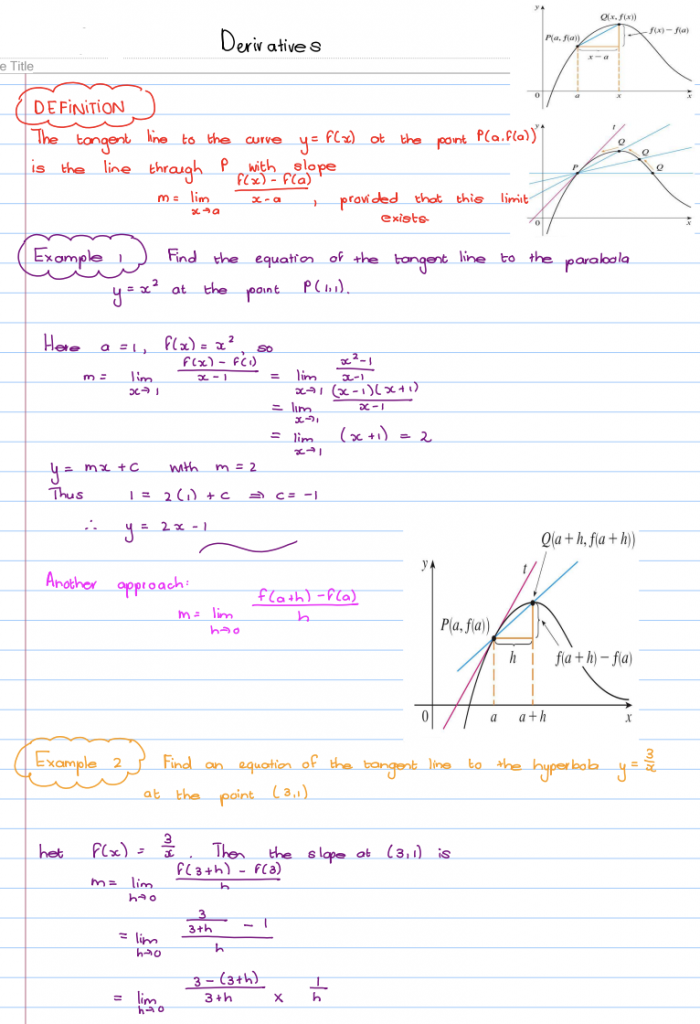
The note introduces the derivative as a function itself, highlighting its role in determining the slope of tangent lines to curves. It discusses various notations representing derivatives, including prime notation, Leibniz’s notation, and differential notation. This comprehensive coverage ensures a thorough understanding of how derivatives can be expressed.

The concept of higher derivatives is then introduced, elucidating how the differentiation process can be repeated to obtain subsequent derivatives. This exploration of higher derivatives is complemented by a collection of useful differentiation formulae that allow for the differentiation of various functions, including polynomials, exponentials, logarithms, and trigonometric functions.

Excerpt:

Derivatives Explained

The note delves into the derivative of trigonometric functions, providing a detailed explanation of the derivatives of sine, cosine, tangent, secant, cosecant, and cotangent functions. This section includes both the theoretical derivation of these derivatives and practical examples that illustrate their application.

The chain rule, a vital tool in calculus, is thoroughly explained in the note. The chain rule allows for the differentiation of composite functions by applying the derivative of the outer function multiplied by the derivative of the inner function. Its application is demonstrated through examples and step-by-step explanations.

Implicit differentiation is introduced as a powerful technique for differential equations that are not explicitly expressed as functions.