Calculus-Based Physics 1 Reference (Grade A)

Summary:

The PHY2048C reference sheet provides critical formulas and explanations for various physics concepts, such as:

1. **Kinematics**: Describes motion using displacement, velocity, acceleration, and time with given formulas like \(𝑣𝑓 = 𝑣0 + 𝑎𝑡\).
2. **Rotational Kinematics**: Addresses angular motion with formulas such as \(𝜔𝑓 = 𝜔0 + 𝛼𝑡\).
3. **Forces**: Explains various forces, including gravitational and frictional forces.
4. **Rotational Forces**: Covers concepts like torque and moment of inertia.
5. **Momentum**: Defines linear and angular momentum and their relationship with force and time.
6. **Power and Efficiency**: Gives formulas for calculating power and efficiency.
7. **General Formulas**: Addresses density and pressure.
8. **Work and Energy**: Explains relationships between work, kinetic energy, potential energy, and gravitational potential energy.
9. **Celestial Movement**: Offers formulas for orbital speed, escape velocity, and orbital periods.
10. **Systems of Particles**: Focuses on the centre of mass and moment of inertia for various shapes.
11. **Simple Harmonic Motion**: Describes the motion of springs and pendulums, offering formulas for frequency, period, and angular velocity.

Variables include but aren’t limited to, mass (m), gravitational acceleration (g = 9.81 \(𝑚/𝑠^2\)), and the gravitational constant (G = 6.67× 10^−11).

Excerpt:

Calculus-Based Physics 1 Reference

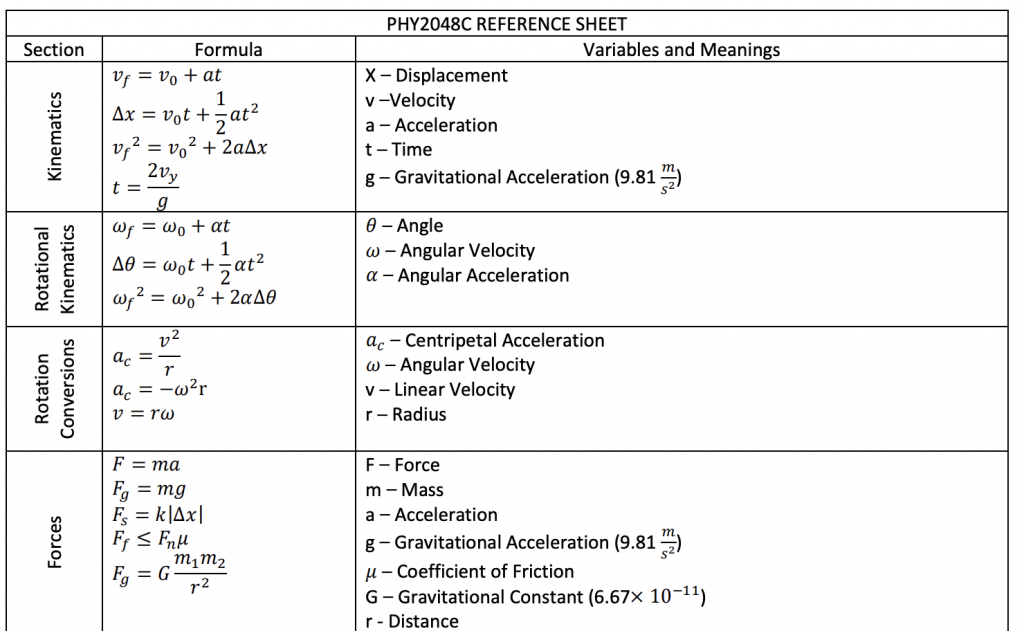
PHY2048C REFERENCE SHEET

SECTION FORMULA VARIABLES AND MEANINGS
——————————————————————————-
Kinematics:
– 𝑣𝑓 = 𝑣0 + 𝑎𝑡 X – Displacement
– ∆𝑥 = 𝑣0𝑡 + 0.5𝑎𝑡^2 v – Velocity
– 𝑣𝑓^2 = 𝑣0^2 + 2𝑎∆𝑥 a – Acceleration
– 𝑡 = 2𝑣𝑦/𝑔 t – Time
g – Gravitational Acceleration (9.81 m/s^2)

Rotational Kinematics:
– 𝜔𝑓 = 𝜔0 + 𝛼𝑡 𝜃 – Angle
– ∆𝜃 = 𝜔0𝑡 + 0.5𝛼𝑡^2 𝜔 – Angular Velocity
– 𝜔𝑓^2 = 𝜔0^2 + 2𝛼∆𝜃 𝛼 – Angular Acceleration

Rotation Conversions:
– 𝑎𝑐 = 𝑣^2/𝑟 𝑎𝑐 – Centripetal Acceleration
– 𝑎𝑐 = −𝜔^2r 𝜔 – Angular Velocity
– 𝑣 = 𝑟𝜔 v – Linear Velocity
r – Radius

Forces:
– 𝐹 = 𝑚𝑎 F – Force
– 𝐹𝑔 = 𝑚𝑔 m – Mass
– 𝐹𝑠 = 𝑘|∆𝑥| a – Acceleration
– 𝐹𝑓 ≤ 𝐹𝑛𝜇 g – Gravitational Acceleration (9.81 m/s^2)
– 𝐹𝑔 = 𝐺𝑚1𝑚2/𝑟^2 𝜇 – Coefficient of Friction
G – Gravitational Constant (6.67× 10−11)
r – Distance

Rotational Forces:
– 𝜏 = 𝑟𝐹𝑠𝑖𝑛(𝜃) 𝜏 – Torque (Rotational Force)
– ∑𝜏 = 𝐼𝛼 r – Distance from the point of Rotation
– 𝐼 = ∫ 𝑟^2𝑑𝑚 θ – Angle concerning Object
𝐼 – Moment of Inertia
𝛼 – Angular Acceleration

Momentum:
– 𝑝 = 𝑚𝑣 p – Momentum
– J = ∆p = F∆t J – Impulse
– 𝐽 = ∫ 𝐹 𝑑𝑡