All Formulas of Trigonometry
Summary:
The study of trigonometry is initiated in the Class 10 Mathematics syllabus through the “Introduction to Trigonometry” chapter. This subject area holds an instrumental role in many disciplines, including but not limited to physics, engineering, and computer science, thereby proving crucial for students inclined towards these fields.
Starting from the basics, the chapter clearly defines an angle. An angle is the measure of rotation that a line segment undergoes with respect to any of its endpoints. This rotation can be either anti-clockwise or clockwise; the former renders the angle positive, while the latter results in a negative angle.
Building upon these fundamentals, the chapter presents the core trigonometric ratios applicable to any right-angled triangle. These ratios include sine (sinθ), cosine (cosθ), tangent (tanθ), cosecant (cosecθ), and secant (secθ). In a right-angled triangle, ‘p’ denotes the perpendicular, ‘b’ represents the base, and ‘h’ is the hypotenuse.
Delving further into the subject, the chapter highlights the precise values of these trigonometric ratios for angles ranging from 0° to 90°. This is an indispensable tool for students to comprehend how these ratios change as the angle varies.
Concluding the chapter, the ideas of ‘line of sight’, ‘angle of elevation’, and ‘angle of depression’ are introduced. The line of sight is drawn from our eyes to an observed object.
Excerpt:
All Formulas of Trigonometry
Maths Formulas For Class 10 Chapter- Introduction To Trigonometry
Class 10 chapter- Introduction to Trigonometry Formula
Introduction and Application of Trigonometry
Definition of Angle If we rotate a line segment with respect to any of its endpoints, the amount of rotation is called an angle. If rotation exists in the anti-clockwise direction, an angle is positive. Otherwise negative.
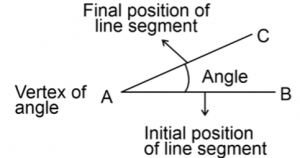
All Formulas of Trigonometry
Trigonometric ratios for any right-angled triangle
sinθ =sinθ, cosineθ = cosθ, tangentθ = tanθ, cosecantθ = cosecθ, secantθ = secθ
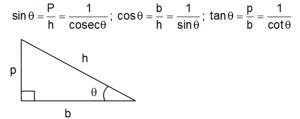
All Formulas of Trigonometry
Where p→perpendicular, h→ hypotenuse, b→ base
Trigonometric Identities
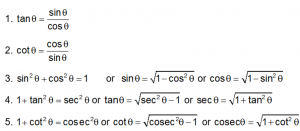
All Formulas of Trigonometry
Values of Trigonometric ratios of 0° to 90°


Reviews